Irrational Numbers

An Irrational Number is a real number that cannot be written as a simple fraction.

Irrational means not Rational

Examples: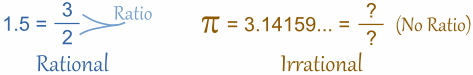

Rational Numbers

OK. A Rational Number can be written as a Ratio of two integers (ie a simple fraction).

Example: 1.5 is rational, because it can be written as the ratio 3/2

Example: 7 is rational, because it can be written as the ratio 7/1

Example 0.333... (3 repeating) is also rational, because it can be written as the ratio 1/3

Irrational Numbers

But some numbers cannot be written as a ratio of two integers ...

...they are called Irrational Numbers.

It is irrational because it cannot be written as a ratio (or fraction), not because it is crazy!

Example: π (Pi) is a famous irrational number.

π = 3.1415926535897932384626433832795 (and more...) You cannot write down a simple fraction that equals Pi.

The popular approximation of ²²/₇ = 3.1428571428571... is close but not accurate.

Another clue is that the decimal goes on forever without repeating.

Rational vs Irrational

So you can tell if it is Rational or Irrational by trying to write the number as a simple fraction.

Example: can be written as a simple fraction like this:

9.5 = ¹⁹/₂

So it is a rational number (and so is not irrational)

Here are some more examples:

Number	As a Fraction	Rational or Irrational?
1.75	7/4	Rational
.001	1/1000	Rational
√2 (square root of 2)	?	Irrational !

Square Root of 2

Let's look at the square root of 2 more closely.

If you draw a square of size "1", what is the distance across the diagonal?

The answer is the square root of 2, which is 1.4142135623730950...(etc)
But it is not a number like 3, or five-thirds, or anything like that ...

Famous Irrational Numbers

	Pi is a famous irrational number. People have calculated Pi to over a quadrillion decimal places and still there is no pattern. The first few digits look like this: 3.1415926535897932384626433832795 (and more ...)
	The number e (Euler's Number) is another famous irrational number. People have also calculated e to lots of decimal places without any pattern showing. The first few digits look like this: 2.7182818284590452353602874713527 (and more ...)
	The Golden Ratio is an irrational number. The first few digits look like this: 1.61803398874989484820... (and more ...)
	Many square roots, cube roots, etc are also irrational numbers. Examples: √3 1.7320508075688772935274463415059 (etc) √99 9.9498743710661995473447982100121 (etc)
But √4 = 2 (rational), and √9 = 3 (rational) ... ... so not all roots are irrational.

Note on Multiplying Irrational Numbers

Have a look at this:

• π × π = π² is irrational
• But √2 × √2 = 2 is rational

So be careful ... multiplying irrational numbers might result in a rational number!

QuickFact : Apparently Hippasus (one of Pythagoras' students) discovered irrational numbers when trying to write the square root of 2 as a fraction (using geometry, it is thought). Instead he proved you couldn't write the square root of 2 as a fraction and so it was irrational.

But followers of Pythagoras could not accept the existence of irrational numbers, and it is said that Hippasus was drowned at sea as a punishment from the gods!