It turns out that (almost) any kind of a wave can be written as a sum
of sines and cosines. So for example, if I was to record your voice for
one second saying something, I can find its fourier series which may
look something like this for example
voice=sin(x)+110sin(2x)+1100sin(3x)+...
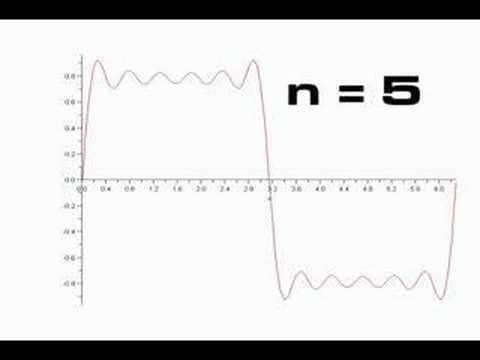
and this interactive module
shows you how when you add sines and/or cosines the graph of cosines
and sines becomes closer and closer to the original graph we are trying
to approximate.
The really cool thing about fourier series is that first, almost any kind of a wave can be approximated. Second, when fourier series converge, they converge very fast.
So one of many many applications is compression. Everyone's favorite MP3 format uses this for audio compression. You take a sound, expand its fourier series. It'll most likely be an infinite series BUT it converges so fast that taking the first few terms is enough to reproduce the original sound. The rest of the terms can be ignored because they add so little that a human ear can likely tell no difference. So I just save the first few terms and then use them to reproduce the sound whenever I want to listen to it and it takes much less memory.
JPEG for pictures is the same idea.
Most audio and image CODECs (including JPEG and mp3) actually use DCTs, which are a subset of generalized Fourier transforms
I was talking about the decrease in the magnitude of fourier coefficients. Basically, the smoother the function is, the faster the fourier coefficients will decrease in magnitude and hence we need fewer terms to approximate the original function well.
One of our undergraduate students was taking data generated by a person running on a force plate. Since force exerted on your feet from running is for the most part periodic, she fit the data with a curve using Fourier analysis. The work that followed can be used to help develop better running shoes.
fourier series is broadly used in telecommunications system, for modulation and demodulation of voice signals, also the input,output and calculation of pulse and their sine or cosine graph.
BTW this is my favourite animation regarding Fourier series
http://bl.ocks.org/jinroh/7524988
The equalizer you see in your audio player is a Fourier representation of the music that you are listening to. (Well not 100% accurate in most cases)
What the Fourier transform indicates is the strength of each frequency component of the signal. It decomposes the signal into its sine and cosine components and its amplitudes.
There are variants of the Fourier transform, which are built around a multitude of engineering applications like Radar data processing (using sound waves to detect stuff..), in medicine where we have Ultrasound and in the Navy where we have SONAR.
In most cases we use the Fourier Transforms discrete counterpart which works on real world data. Measurements made by most modern devices and sensors are discrete. There are several efficient algorithms and in several devices we also have special hardware for this.
The Fourier transform, which converts a signal into a weighted sum of sine waves and then back again, is the secret ingredient that makes all lossy media compression possible!
MP3 is a lossy audio compression algorithm, as is JPEG for still images and MPEG for movies. These centerpiece of these algorithms is the conversion of the audio or image signal into 1D or 2D sine waves, then deleting the parts that "won't be noticed", and then later converting the data back into the original signal with the deleted frequencies missing. (The loss is deliberate and strategically applied to reduce data without reducing perceived quality.)
The Fourier transform is also the key enabling technique for all spread-spectrum wireless data technology, including WiFi, digital cell phone broadcasts, 4G mobile data broadcast, and dynamic bandwidth regulating DSL.
A key difference between the ideal Fourier transform and the way it is applied is that the ideal Fourier transform turns infinitely-long signals into infinitely long sine waves, which on a practical scale is impossible and not useful. The applied Fourier transform uses "wavelets" which are sine waves that quickly taper to zero, representing, for example, a few milliseconds of sound (in MP3) or 8x8 pixel image blocks (in JPEG). An example wavelet:
On your stereo if it has a graphic equalizer. This is a physical hardware implementation of the Fourier Transform.
http://en.wikipedia.org/w
The idea that an arbitrary waveform can be decomposed into sine waves, or that sine waves can be combined to make an arbitrary waveform, is so prevalent in electrical engineering that it is hard to notice. (sort of like the faint lines on graph paper) It's just the way things are done, and thought about. To use a software analogy, it's part of the (standard input & output) module for
electronics.
It is used in almost every modem in the DSP, and in DSL systems as discrete multi-tone modulation.
Fourier's idea shows up once again when we look at a stereo speaker which has a woofer (bass), mid-range, and tweeter (high notes) - the combination of the sounds in the air reproduces the complex music waveform.
https://www.youtube.com/watch?v=k8FXF1KjzY0
The really cool thing about fourier series is that first, almost any kind of a wave can be approximated. Second, when fourier series converge, they converge very fast.
So one of many many applications is compression. Everyone's favorite MP3 format uses this for audio compression. You take a sound, expand its fourier series. It'll most likely be an infinite series BUT it converges so fast that taking the first few terms is enough to reproduce the original sound. The rest of the terms can be ignored because they add so little that a human ear can likely tell no difference. So I just save the first few terms and then use them to reproduce the sound whenever I want to listen to it and it takes much less memory.
JPEG for pictures is the same idea.
Most audio and image CODECs (including JPEG and mp3) actually use DCTs, which are a subset of generalized Fourier transforms
I was talking about the decrease in the magnitude of fourier coefficients. Basically, the smoother the function is, the faster the fourier coefficients will decrease in magnitude and hence we need fewer terms to approximate the original function well.
One of our undergraduate students was taking data generated by a person running on a force plate. Since force exerted on your feet from running is for the most part periodic, she fit the data with a curve using Fourier analysis. The work that followed can be used to help develop better running shoes.
fourier series is broadly used in telecommunications system, for modulation and demodulation of voice signals, also the input,output and calculation of pulse and their sine or cosine graph.
BTW this is my favourite animation regarding Fourier series
http://bl.ocks.org/jinroh/7524988
The equalizer you see in your audio player is a Fourier representation of the music that you are listening to. (Well not 100% accurate in most cases)
What the Fourier transform indicates is the strength of each frequency component of the signal. It decomposes the signal into its sine and cosine components and its amplitudes.
There are variants of the Fourier transform, which are built around a multitude of engineering applications like Radar data processing (using sound waves to detect stuff..), in medicine where we have Ultrasound and in the Navy where we have SONAR.
In most cases we use the Fourier Transforms discrete counterpart which works on real world data. Measurements made by most modern devices and sensors are discrete. There are several efficient algorithms and in several devices we also have special hardware for this.
The Fourier transform, which converts a signal into a weighted sum of sine waves and then back again, is the secret ingredient that makes all lossy media compression possible!
MP3 is a lossy audio compression algorithm, as is JPEG for still images and MPEG for movies. These centerpiece of these algorithms is the conversion of the audio or image signal into 1D or 2D sine waves, then deleting the parts that "won't be noticed", and then later converting the data back into the original signal with the deleted frequencies missing. (The loss is deliberate and strategically applied to reduce data without reducing perceived quality.)
The Fourier transform is also the key enabling technique for all spread-spectrum wireless data technology, including WiFi, digital cell phone broadcasts, 4G mobile data broadcast, and dynamic bandwidth regulating DSL.
A key difference between the ideal Fourier transform and the way it is applied is that the ideal Fourier transform turns infinitely-long signals into infinitely long sine waves, which on a practical scale is impossible and not useful. The applied Fourier transform uses "wavelets" which are sine waves that quickly taper to zero, representing, for example, a few milliseconds of sound (in MP3) or 8x8 pixel image blocks (in JPEG). An example wavelet:
On your stereo if it has a graphic equalizer. This is a physical hardware implementation of the Fourier Transform.
http://en.wikipedia.org/w
The idea that an arbitrary waveform can be decomposed into sine waves, or that sine waves can be combined to make an arbitrary waveform, is so prevalent in electrical engineering that it is hard to notice. (sort of like the faint lines on graph paper) It's just the way things are done, and thought about. To use a software analogy, it's part of the
It is used in almost every modem in the DSP, and in DSL systems as discrete multi-tone modulation.
Fourier's idea shows up once again when we look at a stereo speaker which has a woofer (bass), mid-range, and tweeter (high notes) - the combination of the sounds in the air reproduces the complex music waveform.
https://www.youtube.com/watch?v=k8FXF1KjzY0

















1 comments
Hi may i just ask, how did your student actually develop better running shoes using Fourier's series? Thanks
EmoticonEmoticon